FACTORIZACIÓN

La factorización es el proceso mediante el cual utilizamos dos o más factores, para determinar que el producto sea igual a la expresión dada; tiene como objetivo simplificar una expresión o descomponer factores.

 Ejemplo:

c(c + d) = d2 + cd

                 (x + 5) (x +4) = x2 + 20x + 9

             (a+ b) (a- b) = a2 - ab - b2

Tipos de factorización

 -factor común: ab+ac = a(b+c)

 -Trinomio cuadrado perfecto: a2 – 2ab + b2 = (a – b) 2

 -Trinomios de la forma: x2 + b x + c

 -Trinomio de la forma: ax2 + b x + c

 -Diferencia de cuadrados perfectos:

 -Suma de cubos perfectos

Factor común

Es la expresión donde se multiplica dos o más números para formar un producto.

ab+ac = a(b+c)

Ejemplo 

al descomponer en factores a2 +2a, tienen como factor común a, lo cual se escribe como coeficiente del paréntesis; dentro del paréntesis se escribe los coeficientes de dividir

a2/a= a y 2a/a = a, y tendremos a2+2ª= a(a+2)

Trinomio cuadrado perfecto

Es cuadrado perfecto cuando el producto de dos factores son iguales

                a2 – 2ab + b2 = (a – b) 2

El cuadrado del primero más el doble del primero por el segundo término más el cuadrado del segundo termino

Ejemplo: x2- 4x + 4= (x – 2)2

Trinomios de la forma x2 + b x + c

Al descomponer en dos factores cuyo primer término es la raíz cuadrada del término cuadrático del trinomio

Ejemplo: 

                 X2- 10x+3= (x+5) (x-3)

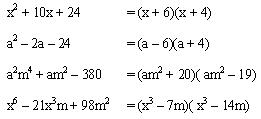
Trinomio de la forma: ax2 + b x + c

Se multiplica el primer coeficiente “a” del factor “ax2” por cada término del trinomio, dejando esta multiplicación indicada en el término “bx” de la manera “b(ax)”, y en el término “ax2” se expresa de esta manera (ax)2

Ejemplo: 

Diferencia de cuadrados perfectos

Consiste en extraer la raíz cuadrada del minuendo y el sustraendo; y se multiplica las raíces por la diferencia entre la raíz del minuendo y la del sustraendo

a2 − b2 = (a + b) · (a – b)

Ejemplo: 

4x2 − 25 = (2x)2 − 52 = (2x + 5) · (2x - 5)

                                         
                                Suma de cubos 

Se descompone dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz.

                           a3 + b3 = (a + b)·(a2 - ab + b2)

Ejemplo: 

                  x3 + 27 = x3 + 33 = (x + 3)·(x2 - 3x + 9)

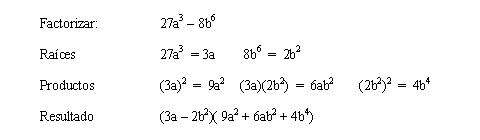
               https://www.youtube.com/watch?v=ROGt8u81FxM